| 大変形時の安定性 |
|
これまで述べてきた積層ゴムに関する理論展開は弾性理論、すなわち微少変形理論に基づいている。実際には天然ゴム材料であっても厳密にはゴムは非線形材料であると同時に、積層ゴムの地震時変形は大変形領域であり、大変形時の剛性算出に際しては材料特性の評価に注意が必要である。特に高減衰ゴム材料は非線形性(ひずみ依存性)が強いため、ひずみ量に応じた材料定数の設定が必要であり、鉛プラグ型では鉛プラグと積層ゴムとの相互作用(中心孔の影響)が不明確な部分もあるため式の適用に際しては注意が必要である。 |
| (12)(13)式で求められる座屈応力度に関しても水平変形をしない状態(水平変形が非常に小さな領域)で水平剛性が0となるときの応力度であり、積層ゴムが大きく変形した状態での座屈応力度ではないことに注意がいる。実際の積層ゴムの設計では、水平変形をした状態で大きな鉛直荷重を支持する必要があり、このときの座屈安定性を確保する必要がある。このような領域での解析として、例えば KohとKellyは積層ゴムの大変形時の力学特性を解析する力学モデルを提案し6)、これに基づいて飯塚は積層ゴムの復元力特性を解析するための大変形マクロモデルを提案7)している。
|
|
ここでは、より簡便な方法で積層ゴムの安定限界状態を表現したい。最初の方法は積層ゴムがせん断変形をした状態の時、有効支持部分( Ae )で全圧縮荷重を支持していると考え、この時の圧縮応力度が座屈応力度に一致する時を安定限界と考える。この場合、座屈応力度と有効支持部面積の関係は |
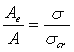 |
| となる。この考え方はとても単純であるが、実験値に比べ非常に安全側の予測をするといわれている。 |
| 2番目の方法は、(12)式中の有効せん断剛性 Ks を求める時に断面積 A の代わりに Ae を用いるというものである。(12)式は次式のように単純化できるので、 |
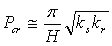 |
| これより、 |
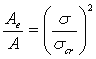 |
| となる。 |
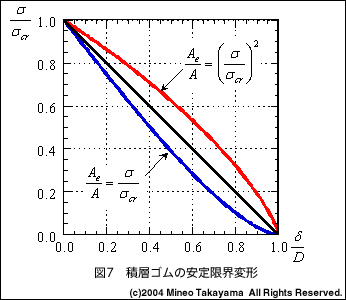
| Ae / A は(6)式から δ / D の関数として表現できる。両手法の関係を描いたものが、図7である。両手法はほぼ同様な関係を示しており、平均的には次式で代表できる。 |
|
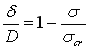 |
(14)
|
|
| 実験結果に比較して両手法は非常に安全側の結果を与えるともいわれているものの、積層ゴムの安定限界を予測する一つの目安になると思われる。ただし、これらの関係を検証するための積層ゴムの形状や材質に応じた実験結果は不足しており、今後のデータの蓄積を期待したい。 |
| 1) |
日本建築学会:"免震構造設計指針(第3版)"、2001 |
| 2) |
多田英之監修:"4秒免震への道"、理工図書、1997 |
| 3) |
P. B. Lindley : "Natural Rubber Structural Bearings", Joint Sealing and Bearing Systems for Concrete Structures, Vol.1, ACI, 1981 |
| 4) |
西村 功ほか:"中空断面を有する積層ゴム支承の鉛直剛性に関する解析的研究"、日本建築学会構造系論文集、第505号、1998.3 |
| 5) |
岩部、高山ほか:"天然ゴム系・高減衰型・鉛プラグ入り積層ゴムのオフセットせん断−引張特性試験"、日本建築学会大会学術講演梗概集、1999.9
|
| 6) |
Koh, C. G., Kelly, J. M. : "A Simple Mechanical Model for Elastomeric Bearings used in Base Isolation", Int. J. Mech. Sci., 30, 1988 |
| 7) |
日本建築学会:"免震構造設計指針(第2版)"、1993 |
|
|