|
応答予測図 |
|
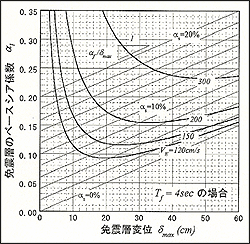
図4に Tƒ を4秒とした時の α1 と δmax の関係を(4)式に基づいて示す。なお、 については平均的に8を使うことができると言われており3)、図4でも κ =8を用いている。 κ =8は、最大変形が起こるまでにダンパーが最大変形下での履歴ループに換算して2サイクル分のエネルギーを吸収したことに対応している。同図(a)は、 Tƒ =4秒に固定した時のベースシア係数と免震層の変形の関係を描いている。下に凸の曲線は入力エネルギー量 VE が一定の時の関係であり、右上がりの直線はダンパーの降伏せん断力係数が一定の時の関係である。 VE の大きさによりベースシア係数が極小となる変形量は変化するものの、 VE =150cm/sでは20〜30cm程度、 VE =300cm/sでは40cm程度の変形となる。なお、免震周期が短くなれば、免震層の変形は小さくなるものの、ベースシア係数が上昇することになる。様々な Tƒ に関して同様の図を描いてみると免震構造の特性をより良く理解できると考える。同図(b)(c)では VE =150cm/sおよび200cm/sと一定にした時の関係図である。免震周期が長くなるに従って、ベースシア係数が小さくなることがわかる。また、ダンパーの降伏せん断力係数、すなわち減衰が小さいと免震層の変形は大きくなり、減衰が大きすぎると変形は小さくなるもののベースシア係数が急激に大きくなる。このように想定される入力地震動の大きさに対して免震構造の応答を最小にするアイソレータの周期とダンパーの減衰量が存在することになる。 |
 |
|
|
図4:免震層のベースシア係数と最大変位の関係
|
| ベースシア係数の最小値 α1min は、 |
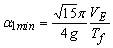 |
(6) |
|
となり、免震周期 Tƒ と入力エネルギーの速度換算値 VE にしか影響されないことがわかる。この時のアイソレータとダンパーのせん断力係数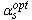 と と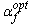 、及び変形量 、及び変形量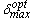 は は |
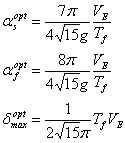 |
(7) |
|
| となる。上式よりアイソレータとダンパーのせん断力の比率 αƒ / αs が8/7とほぼ同じせん断力を負担している時が最適な状態であることが判る。図5には(6)式と(7)式から得られる免震層のベースシア係数と水平変形を示す。免震周期がのびるほど、応答変形は大きくなるものの、ベースシア係数は小さくなり、入力エネルギーの大きさによる変化も小さくなる。 |
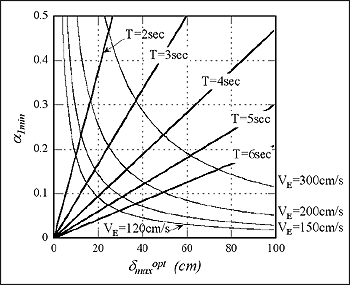 |
図5:免震層のベースシアの極小値とその時の変形量の関係
|
| ベースシア係数の極小値をとる変位は周期が伸びる程、 VE が大きくなる程増加するが、 VE =300cm/sにおいても40cm程度の変形を見込んでおけば良いことがわかる。また免震建物をどの程度の地震入力エネルギー量に対して設計しているのか、又設計されているのかを次式により逆算することも性能を表す1つの指標になると思われる。 |
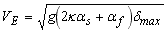 |
(8) |
|
| この様に包絡解析法は免震建物の入力と応答の関係を容易に把握することを可能にする。 |