|
免震層の応答予測式 |
|
ここでは、図3に示すようにアイソレータが弾性、ダンパーが完全弾塑性型の復元力特性を有する場合を対象とする。免震部材には高減衰ゴム系積層ゴムや鉛プラグ型積層ゴムなどのようにダンパーを一体としたデバイスも用いられるが、これらの復元力特性は基本的にバイリニア型でモデル化されており、ここで紹介する方法に適用可能である。また様々な特性を有するデバイスが実用化されているものの、最も単純な復元力モデルを用いて検討しておくことは有効であり適用性も高い。 |
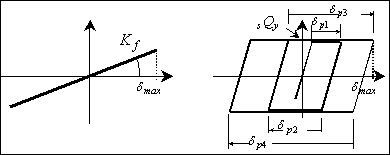 |
図3:アイソレータとダンパーの復元力特性
|
| 最大変形を生じるときのアイソレータとダンパーの吸収エネルギー量はそれぞれ次式で表せる。
|
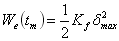 |
(2a) |
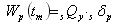 |
(2b) |
|
ここで、Kƒ はアイソレータの水平剛性、 δmax は免震層の最大変形であり、 We はアイソレータの弾性部分の履歴面積を算出している。また、 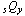 はダンパーの降伏耐力、 はダンパーの降伏耐力、 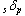 はダンパーの累積塑性変形量である。累積塑性変形量は塑性化領域の変形量(絶対値)を加算することで求められる。 はダンパーの累積塑性変形量である。累積塑性変形量は塑性化領域の変形量(絶対値)を加算することで求められる。 |
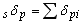 |
| Wp は、降伏体力と累積塑性変形量を乗じることで長方形の履歴面積を求めている。 |
| 累積塑性変形量と最大変形量の関係は、変数 κ を導入することで次式のように表せる3)。 |
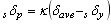 |
(3) |
|
| ここで、 δave は正側と負側の最大変形の平均値、 sδy はダンパーの降伏変位、 κ は累積塑性変形量と最大変形量の比率である。 δave に比べ sδy が十分に小さく、 δave と δmax に大きな差が無ければ(正側と負側に同じ程度の最大変形が発生していれば)、(3)式は sδy= κδmax と近似できる。 |
| この近似式と(2)式を(1)式に代入すれば、次式が得られる。 |
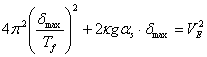 |
| ここで、 VE は地震入力エネルギーの等価速度、M は建物総質量、 g は重力加速度、 Tƒ はアイソレータのみの水平剛性に基づいた周期で次式となる。 |
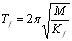 |
| これを αs について解けば、 |
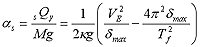 |
| が得られ、これにアイソレータのせん断力係数 αƒ を加えることで、免震層の最大せん断力係数(以下、ベースシア係数) α1 が次式のように求められる。 |
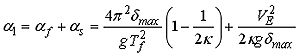 |
(4) |
|
| なお、アイソレータの最大せん断力係数 αƒ は、次式で表せる。 |
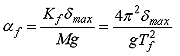 |
| 同様に、免震層の最大変形量 δmax は次式で求められる。 |
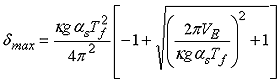 |
(5) |
|